An elliptic curve

Now we turn to cubic curves. The study of these was started by Isaac Newton, but the subject didn't really flourish until somewhat later after the advent of complex analysis. Typical cubics are referred to as elliptic curves, which is bit confusing since they are not actually ellipses. The reason for this name comes from its connection to elliptic integrals and functions, where an integral is called elliptic if the integrand contains a square root of cubic polynomial. Below are a few references in addition to the ones given earlier. A classical reference -- in spite of the name -- is Whittaker and Watson [3]. The first two books are more modern.

Husemoeller, Elliptic curves,
Silverman, The arithmetic of elliptic curves,
Whittaker and Watson, A course in modern analysis.

Let us start with the specific elliptic curve

y2 = 4x3 - x = 4x(x - 1)(x +1)

When x and y are treated as real variables, the graph of the above equation looks like:

After adding a point at infinity to the curve on the right, we get two circles topologically. Now let us treat the variables x and y are treated as complex. (In fact, historically signifcant progress in the study of elliptic integrals was made only after the introduction of complex analysis in the 19th century.) Now the above equation defines a complex elliptic curve which topologically is just a torus (after adding a point at infinity). The two real circles are marked in red here and below. We will also keep track of transevrse circle in yellow. It may be helpful to think of this as a "purely imaginary" curve, even though this isn't quite accurate.

The standard way to see this is by using elliptic functions. These are doubly periodic functions with the mildest possible (i.e. inessential) singularities. A function on the complex plane is doubly periodic if its graph repeats itself in both the horizontal and vertical directions. More precisely, we should be able to tile the plane into equally sized parallelograms (called period parallelograms), such that the piece of the graph over each tile is the same. The simplest nonzero example ( in spite of the complicated formula), with period parallelogram having corners at 0, α₁,α₂ and α₁ + α₂, is the Weierstrass ℘-function

∑ [ ] ℘(t) = t-+ -------1-------- -----1------ t2 (m,n)∈Z2-(0,0) (z - m α1 - nα2)2 (m α1 + n α2)2

Just as we used trignometric functions to parameterize the circle, we can use elliptic functions to parameterize elliptic curves. The above curve is given by the parameterization

x = ℘(t),y = ℘ ′(t)

for t

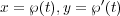
C , where the periods are expressed by the elliptic integrals

∫ ∞ ω1 = √--dx---= 1.8540... 1∕2 4x3 - x

∫ -1∕2---dx--- ω2 = i -∞ √4x3---x-= 1.8540...

(See [Whittaker-Watson, p. 444]). Since these parameterizing functions are doubly periodic, the elliptic curve can be identified with a period parallelogram (in fact a square in this case) with the sides glued together i.e. a torus. Note that the corners of the parallelogram get identified to the same point "at infinity" on the torus.

At this point we can ask whether there exists a rational parameterization of an elliptic curve. The answer is NO. Suppose we could. Then it is possible to show that this extends to a finite to one map of the Riemann sphere (C ∪∞) onto a torus. But this is impossible. The justification of this last statement requires a bit of topology. A version of the Jordan curve theorem says that any closed curve on the sphere would seperate it into two parts (an interior and exterior). If we could find a map as above, we could conclude the Jordan curve holds for the torus: lift the curve up to the sphere and then map the interior/exterior back down. However, it is clear that this isn't true. Just look at the yellow or red curves above.

Even though, we now know the elliptic curve abstractly, we really want understand the way it is embedded into C². As above, we can get a sense of it projecting to 3 real dimensions. The graph of

x1 = Re(℘(t)),x2 = Im(℘(t)),x3 = Re(℘′(t))

represents a projection of the ellptic curve down to R³. For the domain of t, we use a period parallegram. We've colour coded it, and will use the same colour scheme on all the remaining graphs. Also we've marked certain horizontal and vertical lines in red and yellow. The last couple of lines are bisectors. These lines clearly map to the above curves on the torus. Furthermore, these red lines really do map to the real curves because ℘ and its derivative can be shown to take real values along them [Whittaker-Watson p. 444]. Graph

With this preparation, we can now plot the graph. To get a better sense of it, we can generate an animation where it rotates about the x₃-axis:

Click on picture to start animation. The colours of the domain and the graph match. The red curves are the real part of the graph considered at the beginning. Note the local topology near the branch points (- 1
2

,0,0) ... is same as in the first example y² = x. In particular, the singularities in the graph are artifacts of the projection. The elliptic curve has none: it's just a torus as we saw. For example, the yellow curve which is really a loop on the torus gets crushed down to a line in the projection. To get more insight we can use a different projection. Or better yet, use a family of orthogonal projections:

′ x1 = Re(℘(t)),x2 = Im(℘(t)),x3 = Im(℘ (t))

The original projection corresponds to θ = 0. As θ oscillates between 0 and π∕2, we we see the yellow curve open up into a loop and collapse, while the red curves do the opposite.

Click on picture to start animation. For the final graph, we give a top down view with θ = π∕5. Graph

Return to first page. Go to next page.