Elliptic Curve

—-

We start with the curve

y2 = 4x3 - x = x(2x- 1)(2x + 1)

When x and y are treated as real variables, the graph looks like:

...

Things get more interesting when the variables x and y are treated as complex. Then this defines an elliptic curve. (It’s not an ellipse of course. The reason for this name. comes from it connection to elliptic integrals and functions. A classical reference is Whittaker and Watson, “A course in modern analysis”. Modern refernces are the books by Husemullor, Knap, Silverman... on Elliptic Curves). Since the graph would live in C² which has 4 real dimensions, it is impossible visualize completely. Nevertheless, we can project this image to 3 dimensions. To do this, we use the parameterization

x = ℘(t),y = ℘ ′(t)

where t

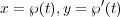
C and ℘ is the Weirstrass ℘-function for an appropriate lattice. This is a elliptic (or doubly periodic) function:

...

The graph of

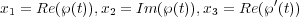
′ x1 = Re(℘(t)),x2 = Im(℘(t)),x3 = Re(℘ (t))

represents the projection down to R³.

....

x1 = Re(℘(t)),x2 = Im( ℘(t)),x3 = (cosθ)Re(℘′(t))+ (sinθ)Im(℘′(t))

—– The corners of the parallelogram can be taken to be 0, α₁,α₂ and α₁ + α₂ where

∫ α = 2 ∞ √--dx----= 3.7081 ... 1 1∕2 4x3 - x

∫ - 1∕2---dx--- α2 = 2i -∞ √4x3-- x-= (3.7081 ...)i

—- θ and π∕2 or θ = 0.

∑ [ ] ℘(t) = 1-+ -------1-------- ------1----- t2 (m,n)∈Z2-(0,0) (t- mα1 - nα2)2 (m α1 + nα2)2

————

As a warm up, we start with a standard example y² = x. When x,y are treated as real variables, this is simply a parabola opening sideways. Things get more interesting when the variables are allowed to take complex values. Since the graph would live in 2 complex or 4 real dimensions, it is impossible visualize completely. Nevertheless, we can get a sense of it projecting to 3 real dimensions. by x₁ and x₂ to be real and imaginary parts of x, and x₃ to be the real part of y. In polar coordinates, this gives

x = Re( √reiθ) = √rcos(θ∕2) 3

We can now plot the graph, using colour to encode the imaginary part of y.

Note that θ runs from 0 to 4π. Branch points (0,0,0), (± 1
2 ,0,0) are .... We will use x_i as coordinates of R³. ...

A a point of a curve f(x,y) = 0 is called singular if the gradient vanishes there. This means that the tangent line cannot be defined. The curves considered previously have no singular points. A nodal cubic

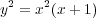
2 2 y = x (x+ 1)

has a singular point at the origin. This is clearly visible from the graph over reals, where we see two tangent directions at the origin.

— In order to plot the complex graph, we reparameterize it by “blowing up” the singularity. This means that seperate the lines at the origin, by introducing a new variable t = y∕x representing the slope each line. Plotting this in x,y,t space yields the so called resolution of singularities depicted in black:

—- We can find an explicit parameterization by subsituting y = xt into

y2 - x2(x+ 1) = 0

yields

x2(t2 - x- 1) = 0

which has two components given by

x = 0,y = 0,z = t

depicted in green, and

2 3 x = t - 1,y = t - t,z = t

in black.

Setting t = r + is, and letting

x1 = Re(x) = r2 - s2 - 1

x2 = Im(x) = 2rs

x3 = Re(y) = r3 - 3rs2 - r

and encoding Im((y) as the colour leads to

—

Notice that the graph looks similar to the graph of the elliptic curve above. This is because the nodal cubic can be viewed as limit of elliptic curves

2 y = x(x + ε)(x +1)

as ε → 0.

———

A hyperelliptic curve is defined by an equation y² = p(x) where p(x) is a polynomial of degree at least 5 with distinct roots. General theory tells us that this would have large genus (i.e. many holes) and that it could parameterized by a automorphic functions. Making this explicit enough to graph would be a daunting task. So we look at the simplest case where all the roots come together y² = x⁵. This is a higher order cusp. We can parameterize this by x = t², y = t⁵. Switching to polar coordinates and taking real and imaginary parts as above, leads to

x1 = r2 cos2θ

2 x2 = r sin2θ

x = r5 cos5θ 3

This yields

——–

For example a plot of

2 y = x(x - 1)(x - 2)(x - 3)(x- 4)

—-

We say that two conics are equivalence if we can transform one to the other by an affine transformation

x → ax+ by + c

y → dx+ ey+ f

Up to equivalence, there are only 4 possibilities

x² + y² = 1

In order to plot this, we start with the usual parameterization

x = cos(θ),y = sin(θ)

and then substitute θ = s + it. From standard identities, we obtain

x = cos(s)cosh(t)- isin(s)sinh(t)

y = sin(s)cosh(t)+ isinh(s)cos(t)

Plotting real and imaginary parts of x and the real part of y yields

—–

The above parameterization of the circle uses transcendental functions. There is another, perhaps less well known, parameterization using only rational functions. Naturally this is refered to as a rational parameterization. The idea is choose a point P on the circle, and parameterize the lines through it by their slope t. These should cut the circle in another point, which can then be expressed in terms of t. Picking P = (0,1), we see that t = (y - 1)∕x. Solving for y and then substituting into the equation for the circle gives

2 2 x + (xt+ 1) = 1

Supposing x ⁄= 0 which typically the case, we get

x = -- 2t t2 + 1

-- 2t2 y = t2 + 1 + 1

We didn’t use this for the plotting, because it’s less convenient (we would need t = ∞ to complete the circle). However, it has other uses. Suppose that we wanted find all right angle triangles with integer sides.This equivalent to finding positive integer solutions for a² + b² = c². Via the substitution x = a∕c, y = b∕c, this is amounts to finding points on the circle with positive rational coordinates. Here’s a very simple procedure: Choose a rational number -1 < t < 0, and substitute into the above formulas.

—

C ∪∞

∇f

——

∣x∣² + ∣y∣² = ε

————————

2 (y - x(x- 1)(x- 2))(5y - x)+ εx = 0

For small ε ⁄= 0 this becomes a

——–

In general if g(d) is the genus of a degree d nonsingular curve, then prodceding as above leads to an inductive formula

g(d+ 1) = g(d)+ d- 1

from which we get

(d- 2)(d - 1) g(d) = (d - 2)+ (d - 1)+ ...1 = ------------ 2