Examples from Lesson 25

Here are some pictures that go along with the examples from the Lesson 25 notes.

Example 1

The cone \( x = \sqrt{y^2+z^2}, \, 0\le x\le 2, \) oriented in the direction of the positive \(x\)-axis. The boundary curve \(\partial S\) is the circle \(y^2+z^2 = 4,\, x=2\) oriented counter-clockwise when viewed from the positive \(x\)-axis.

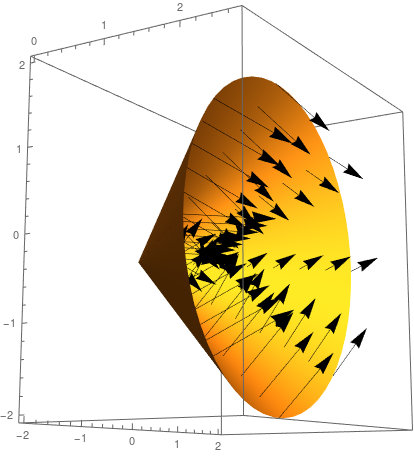
Example 2

The half of the ellipsoid \( 4x^2 + y^2 + 4z^2 = 4 \) that lies to the right of the \( xz \)-plane, oriented in the direction of the positive \(y\)-axis. The boundary curve \(\partial S\) is the circle \(x^2+z^2=1,\, y=0\) oriented clockwise in the \(xz\)-plane.

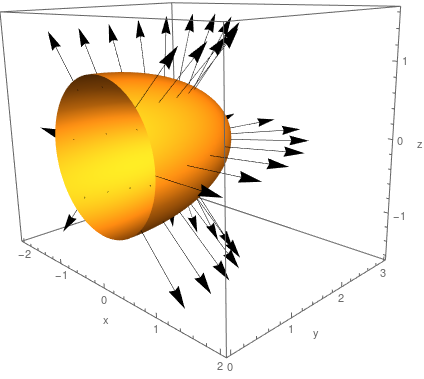
Example 3

The graph below is the region between the plane \(z = y+2\) and the cylinder \(x^2+y^2 = 1\). The surface \(S\) is the plane \(z=y+2\) within the cylinder. The curve \(C = \partial S\) is an ellipse.

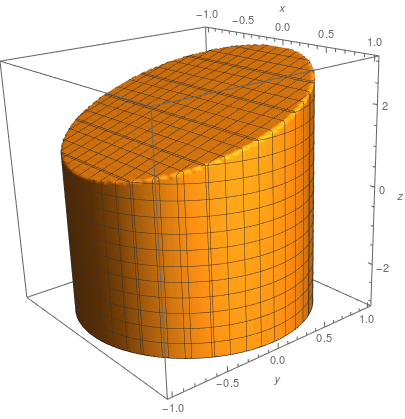
Example 4

Graphs of the cylinder \(x^2 + y^2 = 1\) and the hyperbolic paraboloid \(z = x^2 - y^2\). The surface \(S\) is the part of the hyperbolic paraboloid within the cylinder.

Curve of intersection of the above surfaces, given by the vector equation \(\mathbf{r}(t) = \left<\cos u, \sin u, \cos 2t \right>\). This is the boundary curve \(\partial S\).