Colleen Delaney

Zesting and the relative complexity of Reshetikhin-Turaev invariants

with Calvin McPhail-Snyder, arXiv:2608.02795

We show that there is a polynomial-time Turing equivalence of the Reshetikhin-Turaev invariants of simply-colored framed links whose underlying ribbon fusion categories are related by zesting. Along the way we give a characterization of the zest invariant of a link as a rack cocycle invariant, which shows that zesting "twists" TQFT link invariants by "classical" link invariants familiar from knot theory. Applied to unitary modular fusion categories, our results give a precise sense in which the anyons of topological orders related by zesting generate the same computational complexity.

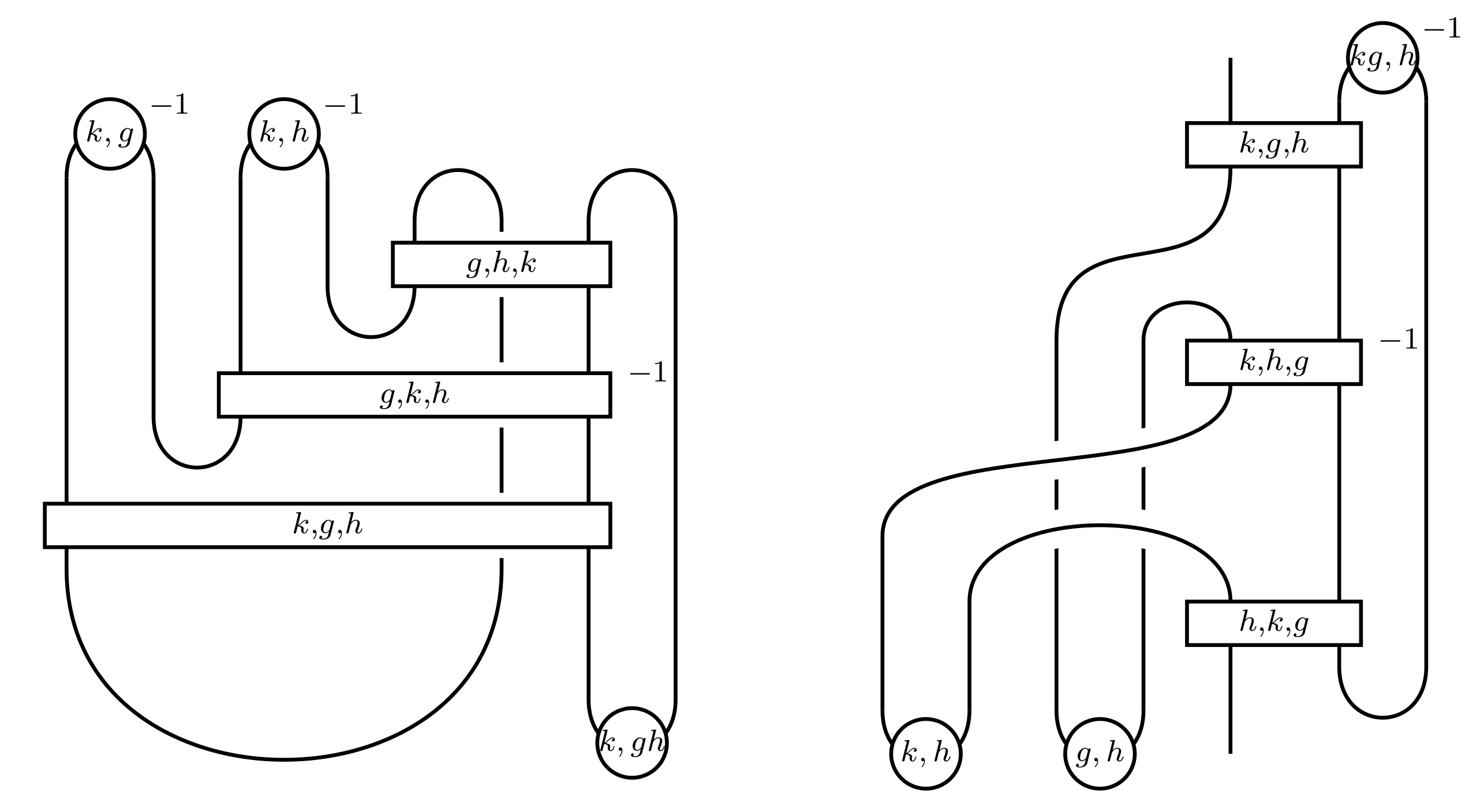
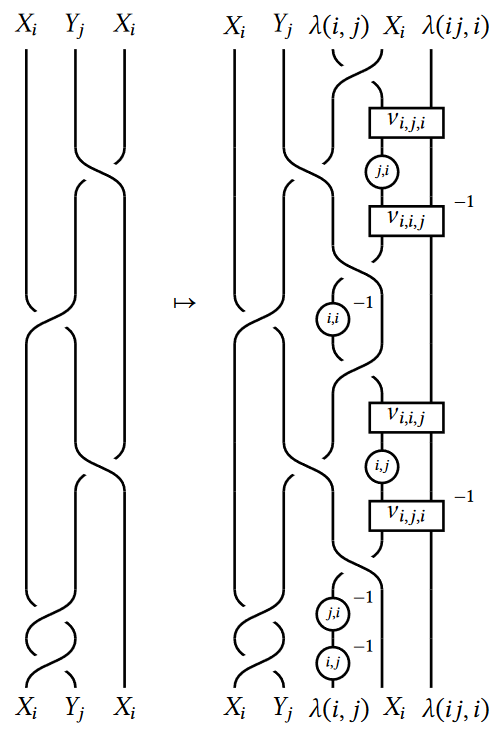
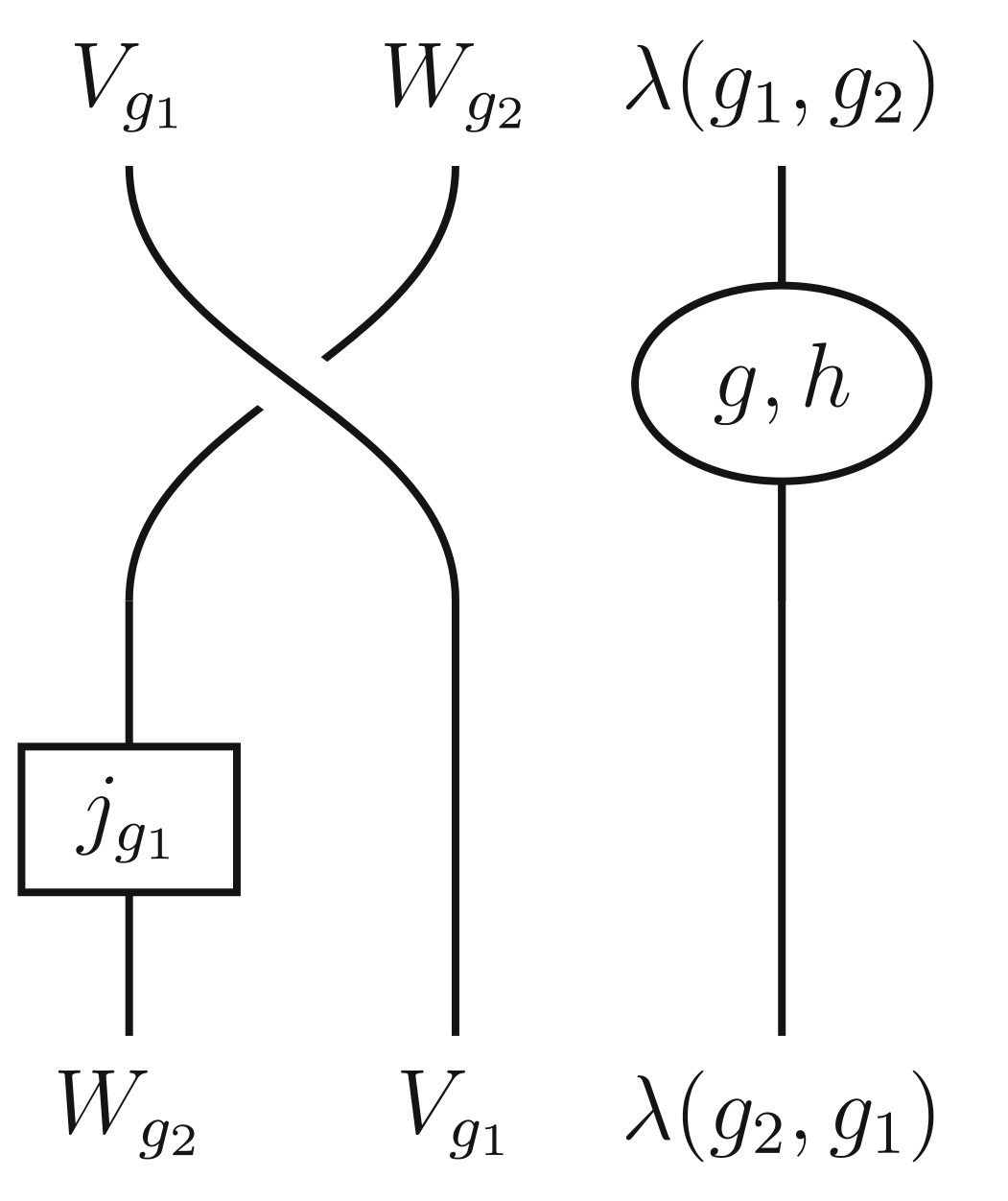
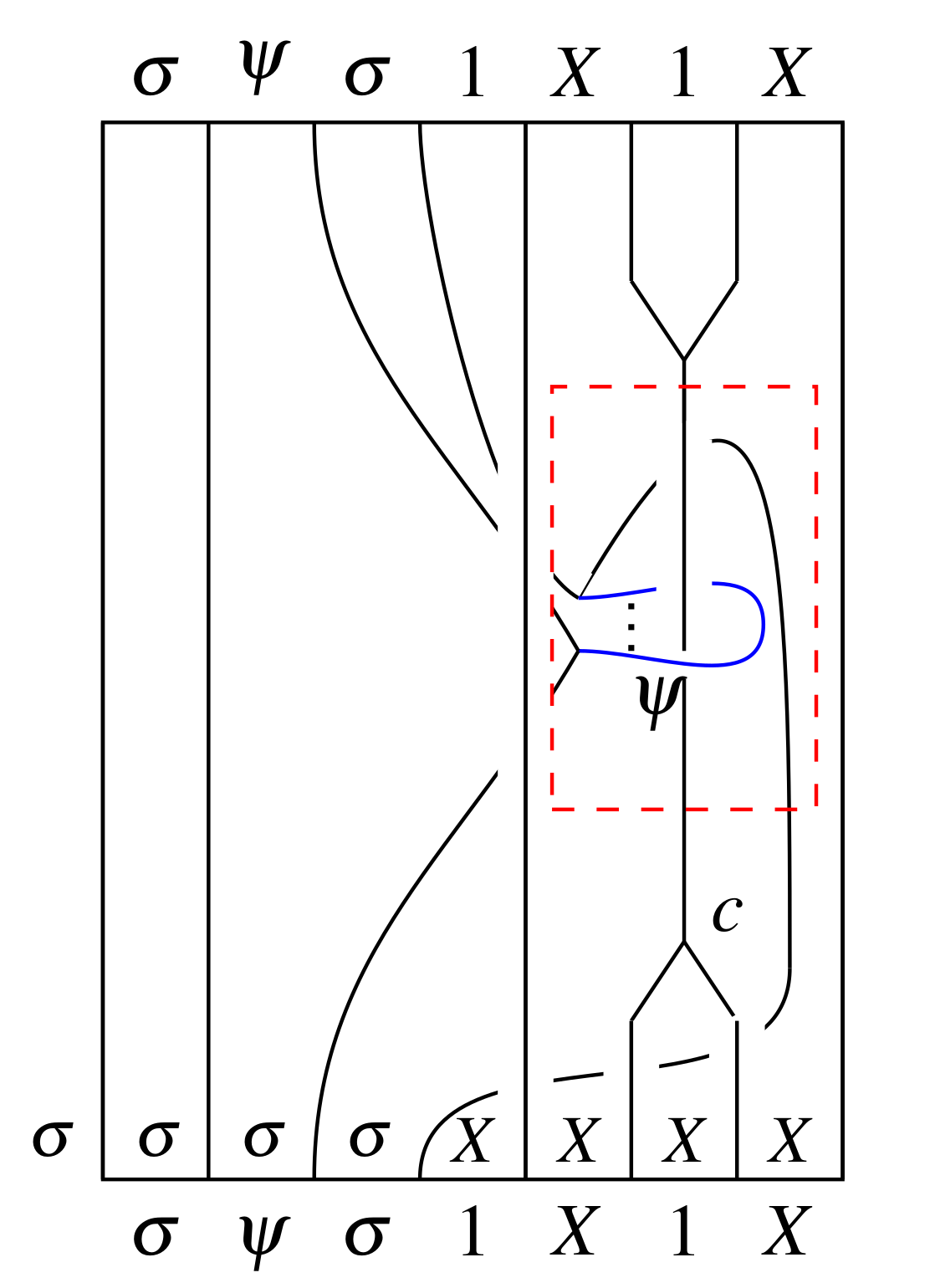
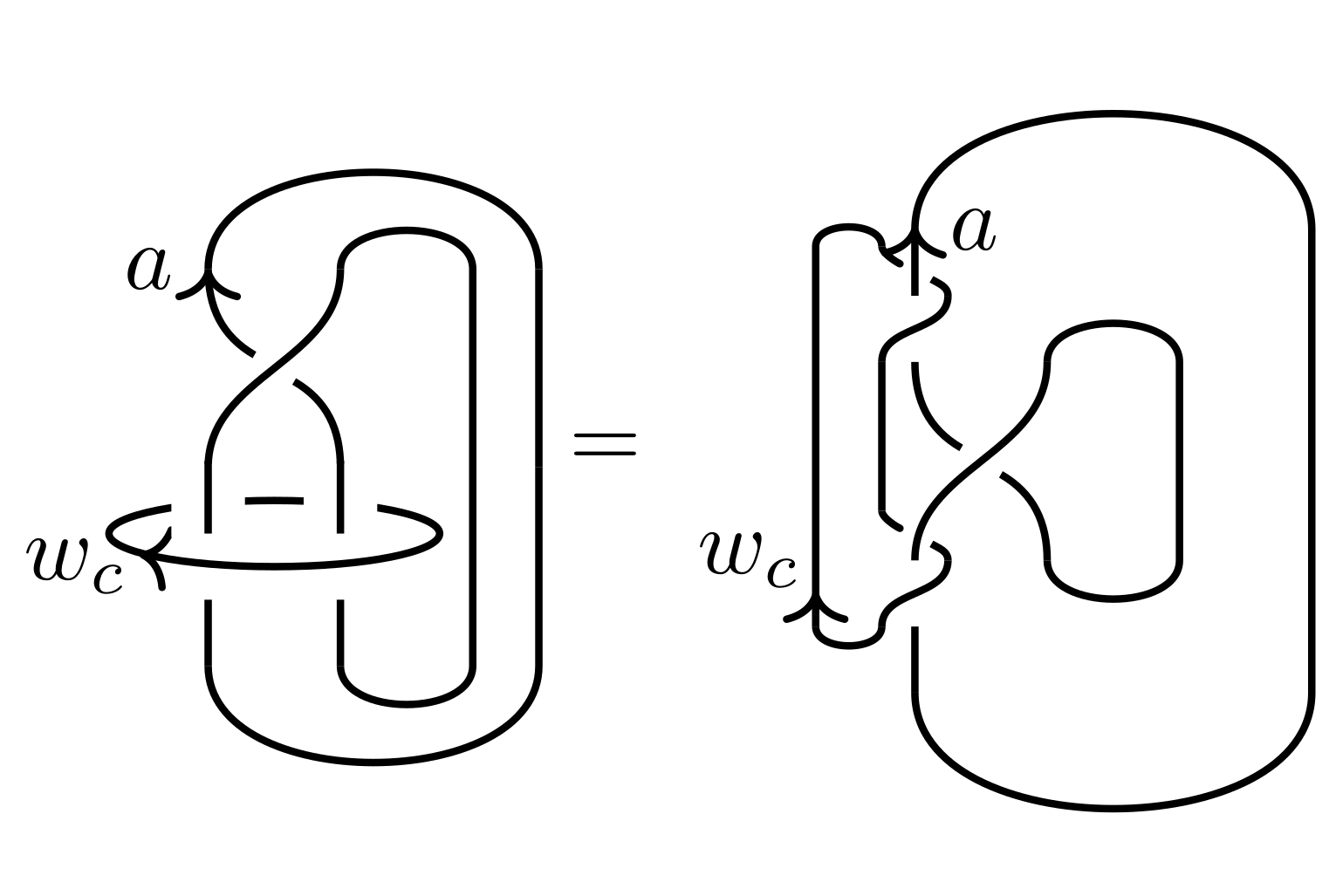
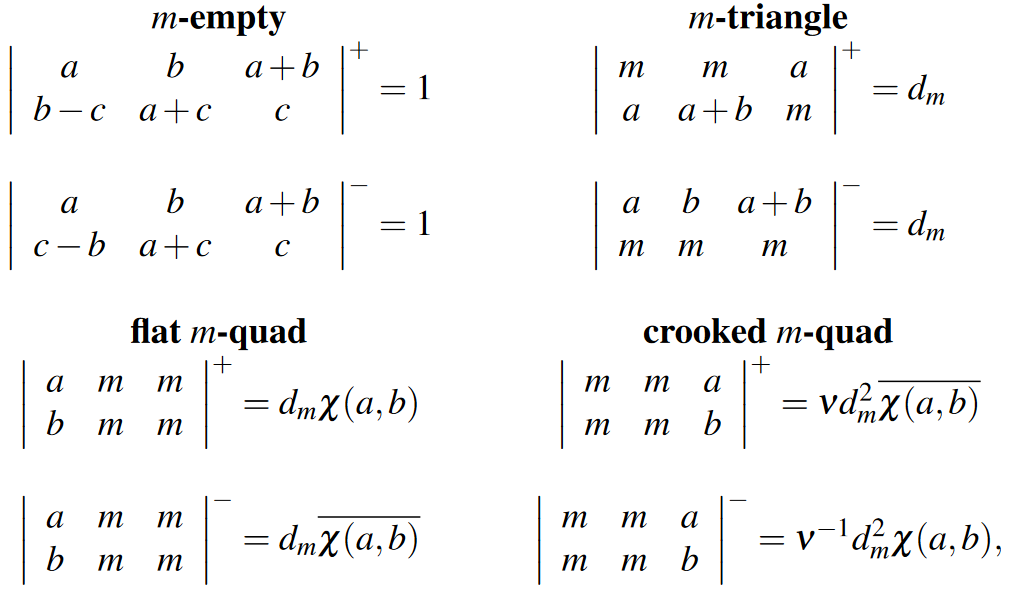The condensed fiber product and zesting

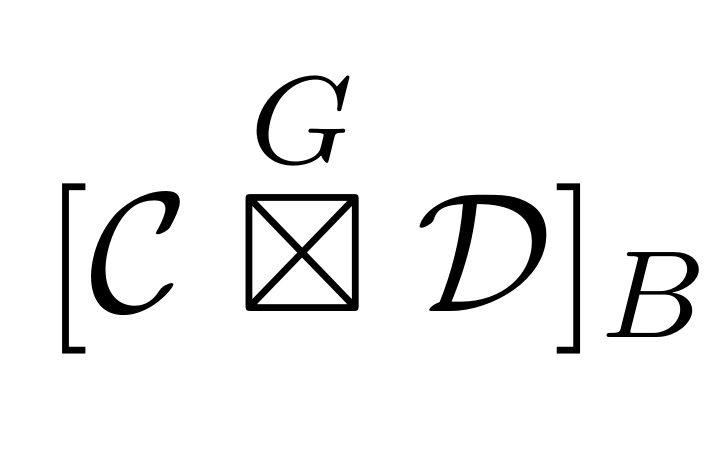
with César Galindo, Julia Plavnik, Eric Rowell, and Qing Zhang, arXiv:2410.09025, Advances in Theoretical and Mathematical Physics. (2026)

We introduce the condensed fiber product of two G-crossed braided fusion categories, explore the relationship with zesting, and touch briefly on the overlap with the hierarchy construction for topological order. We show the condensed fiber product defines a monoidal structure on the 2-category of G-crossed and braided extensions of braided categories with a fixed transparent symmetric pointed subcategory.

Rado matroids and a graphical calculus for boundaries of Wilson loop diagrams

with Susama Agarwala and Karen Yeats, arXiv:2401.05592, Python code, Journal of Mathematical Physics. (2025)

Wilson loop diagrams (a sort of dual to Feynman diagrams) are an ingredient in the recipe for amplitudes in N=4 supersymmetric Yang Mills theory - each diagram specifies a positroid that appears in the definition of the Feynman integral. The boundaries of these positroid cells play a role in the analysis of the Feynman integrals.

We define generalized Wilson loop diagrams (gWLDs) that encode these positroid cell boundaries of ordinary Wilson loop diagrams and introduce a graphical calculus to compute them. Our framework is sufficiently general to generate the boundaries of all Wilson loop diagrams on two propagators and the codimension 1 boundaries for three propagators, but we do expect one can generalize these tools to work for arbitrary numbers of propagators.

An algorithm for Tambara-Yamagami quantum invariants of 3-manifolds, parameterized by the first Betti number

with Clément Maria and Eric Samperton, arXiv:2311.08514, SoCG 2025.

We show that the Turaev-Viro-Barrett-Westbury state-sum invariants that arise from Tambara-Yamagami categories are efficient to compute for 3-manifolds with bounded first Betti number. One can interpret this to mean that any contribution to the hardness of computing these TQFT invariant comes from classical 3-manifold topology rather than something manifestly "quantum".

Zesting produces modular isotopes and explains their topological invariants

with Sung Kim and Julia Plavnik, arXiv:2107.11374, Quantum Topology. (2025)

We show that modular isotopes -- different modular fusion categories with the same modular data -- can be constructed from zesting. Along the way we show that the Reshetikhin-Turaev invariants of framed links factorize under zesting. This implies that you can compute the topological invariants of anyons produced by zesting in a straightforward way.

G-crossed braided zesting

with César Galindo, Julia Plavnik, Eric Rowell, and Qing Zhang, arXiv:2212.05336, J. London Math. Soc. (2024)

We define a generalization of the zesting construction for braided fusion categories on G-crossed braided fusion categories. It turns out that our original notion of braided zesting data is equivalent to the data of a G-crossed braided zesting with the address promise of a trivialization of the G-action functor. This relates zesting topological order to the idea of changing the symmetry fractionalization class of defects in a symmetry-enriched topological (SET) order

Braided zesting and its applications

with César Galindo, Julia Plavnik, Eric Rowell, and Qing Zhang, arXiv:2005.05544, Communications in Mathematical Physics. (2021)

We give a rigorous development of the construction of new braided fusion categories from a given category known as zesting. This method has been used in the past to provide categorifications of new fusion rule algebras, modular data, and minimal modular extensions of super-modular categories.

Symmetry defects and their application to topological quantum computing

with Zhenghan Wang, arXiv:1811.02143, AMS Contemporary Mathematics Series. (2020)

We discuss some examples of qudits encoded in the collective state space of anyons and defects and the quantum gates resulting from braiding them using the formalism of G-crossed modular fusion categories.

On invariants of modular categories beyond modular data

with Parsa Bonderson, César Galindo, Eric Rowell, Alan Tran, and Zhenghan Wang arXiv:1805.05736, Journal of Pure and Applied Algebra. (2020)

We study topological invariants of modular fusion categories that are beyond the modular data (S-matrix and twists), with an eye towards a simple set of complete invariants for modular categories. Our focus is on the W-matrix -- the quantum invariant of a colored framed Whitehead link from the associated TQFT of a modular category. We prove that the rank 49 Mignard-Schauenburg modular categories can be distinguished by the twists together with the W-matrix.