Optimal Transport: the back-and-forth method

This page illustrates the method proposed in: A fast approach to optimal transport: The back-and-forth method [1]. Matlab code for the back-and-forth method can be found on GitHub.

Videos

The following videos illustrate the displacement interpolation [2] between two probability densities supported on a square.

Jack-o'-lantern to pegasus (High resolution version [2048x2048].)
Monge to Kantorovich (High resolution version [2048x2048].)
Rectangle to ring. (High resolution version [2048x2048])
Pikachu to Raichu. (High resolution version [2048x2048])
Caffarelli's counterexample [3]. (High resolution version [2048x2048])
Santambrogio–Wang's convexity counterexample [4]. (High resolution version [2048x2048])

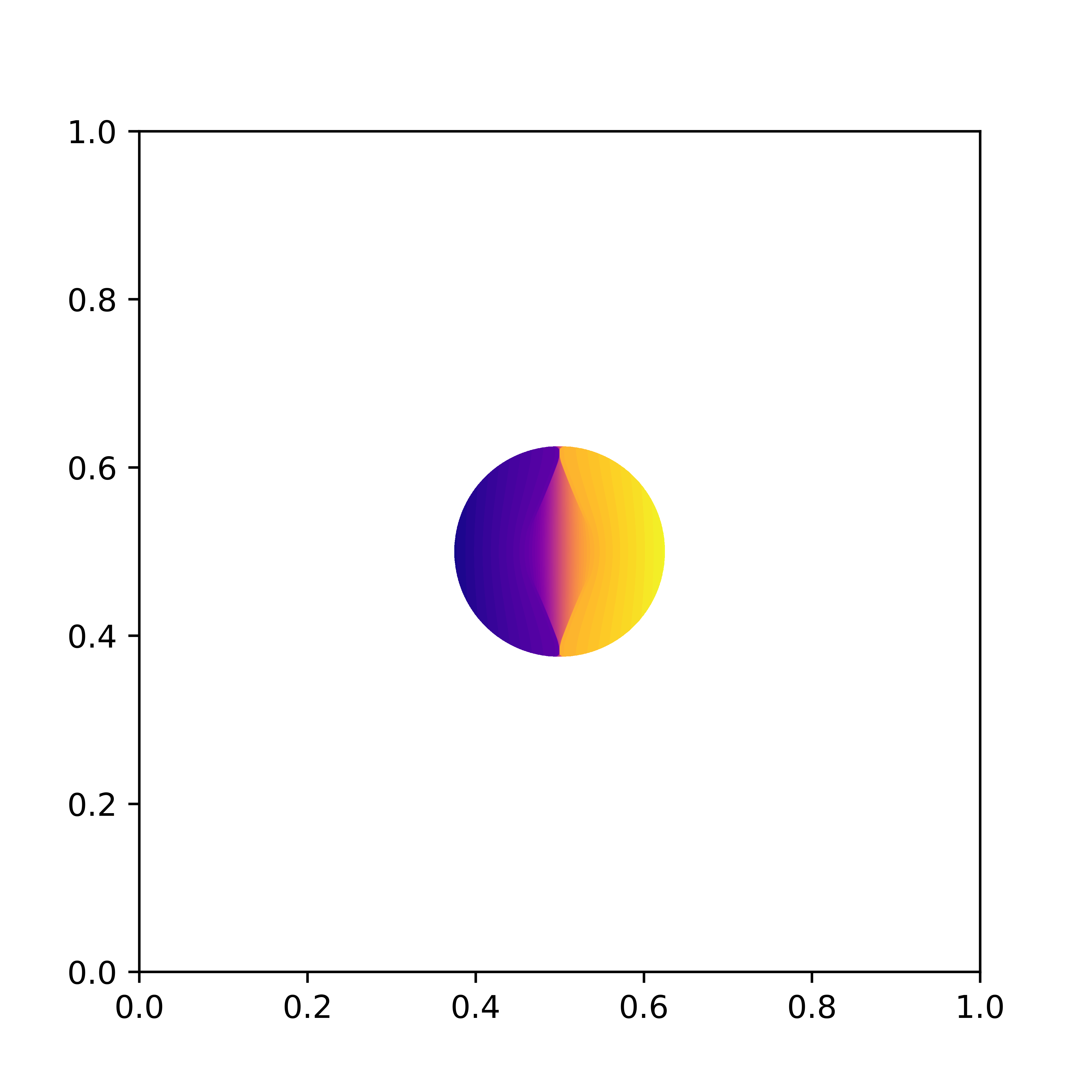
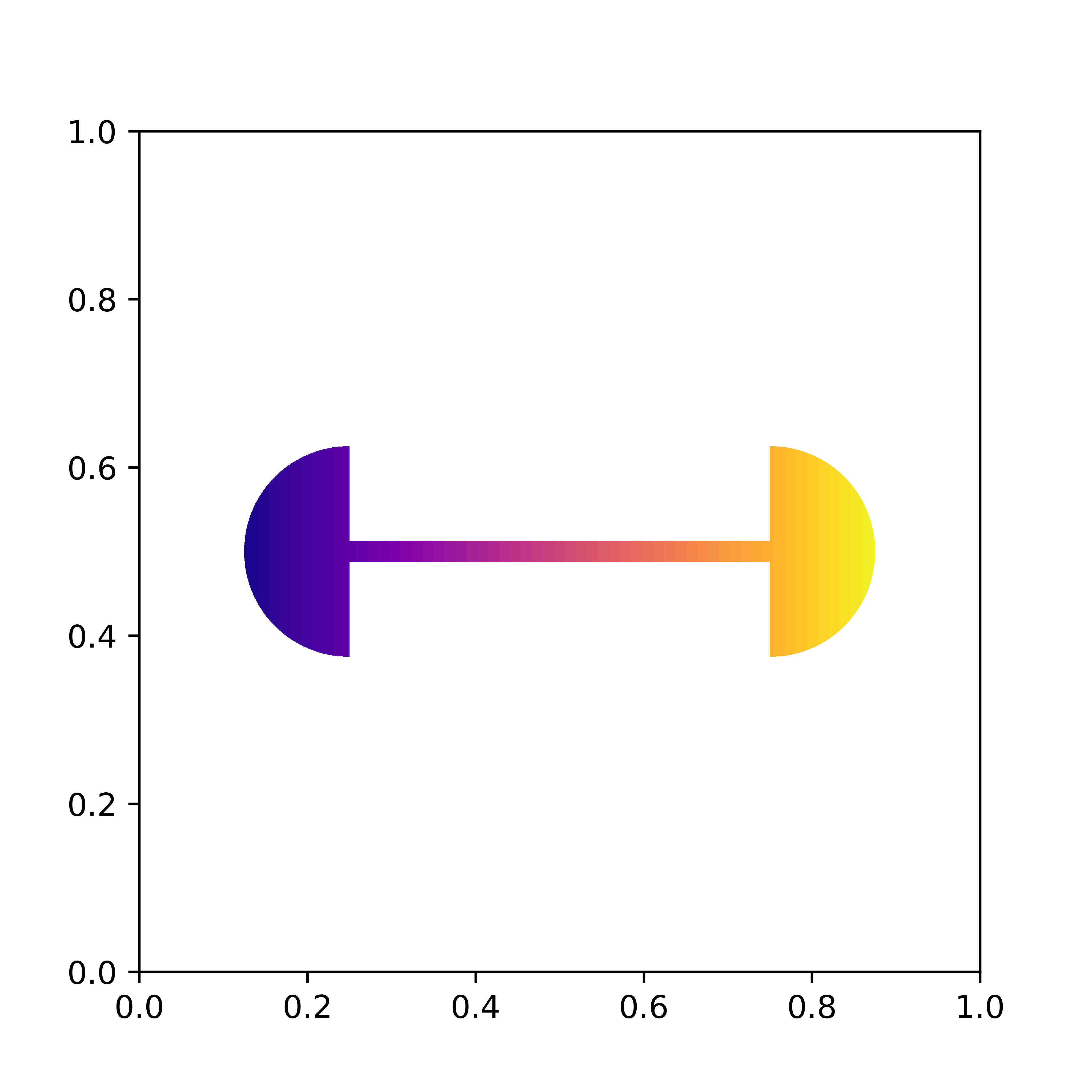
Caffarelli's counterexample

In [3] Caffarelli showed that the optimal transport map can be discontinuous when a measure is supported on a non-convex domain.

Caffarelli's xMap
Support of the initial density. Colors represent the mapping from initial density to final density.
Caffarelli's xMap
Support of the final density.

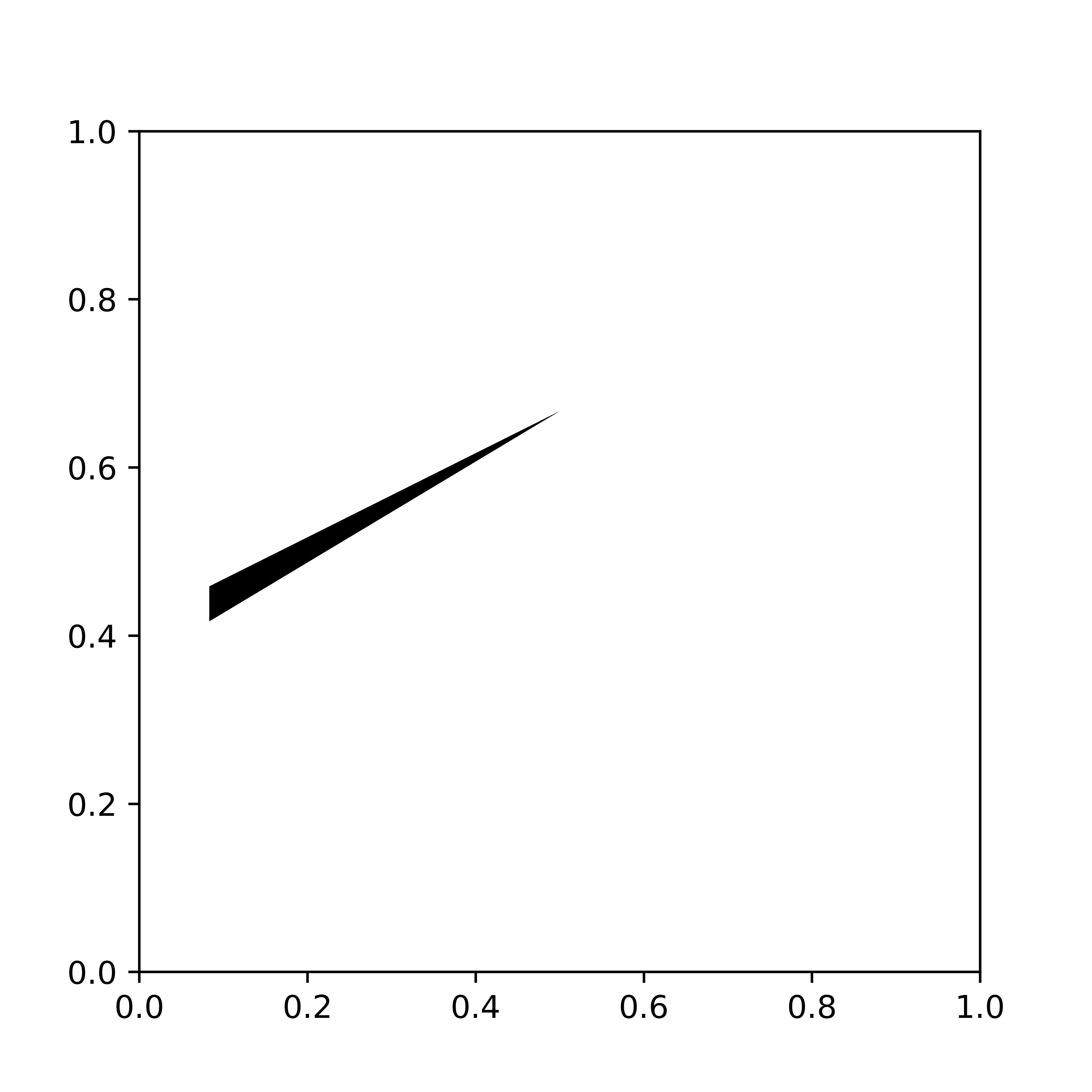
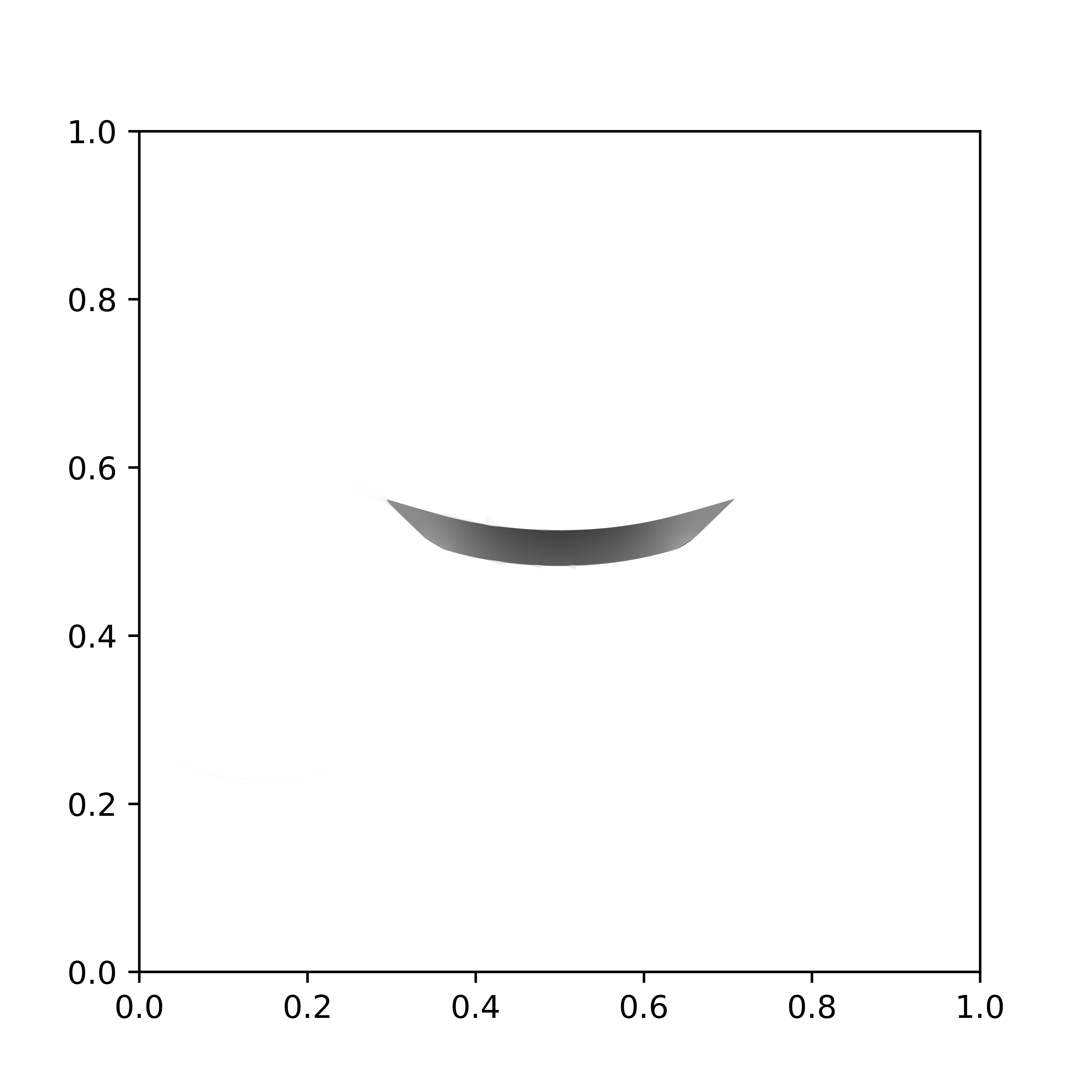
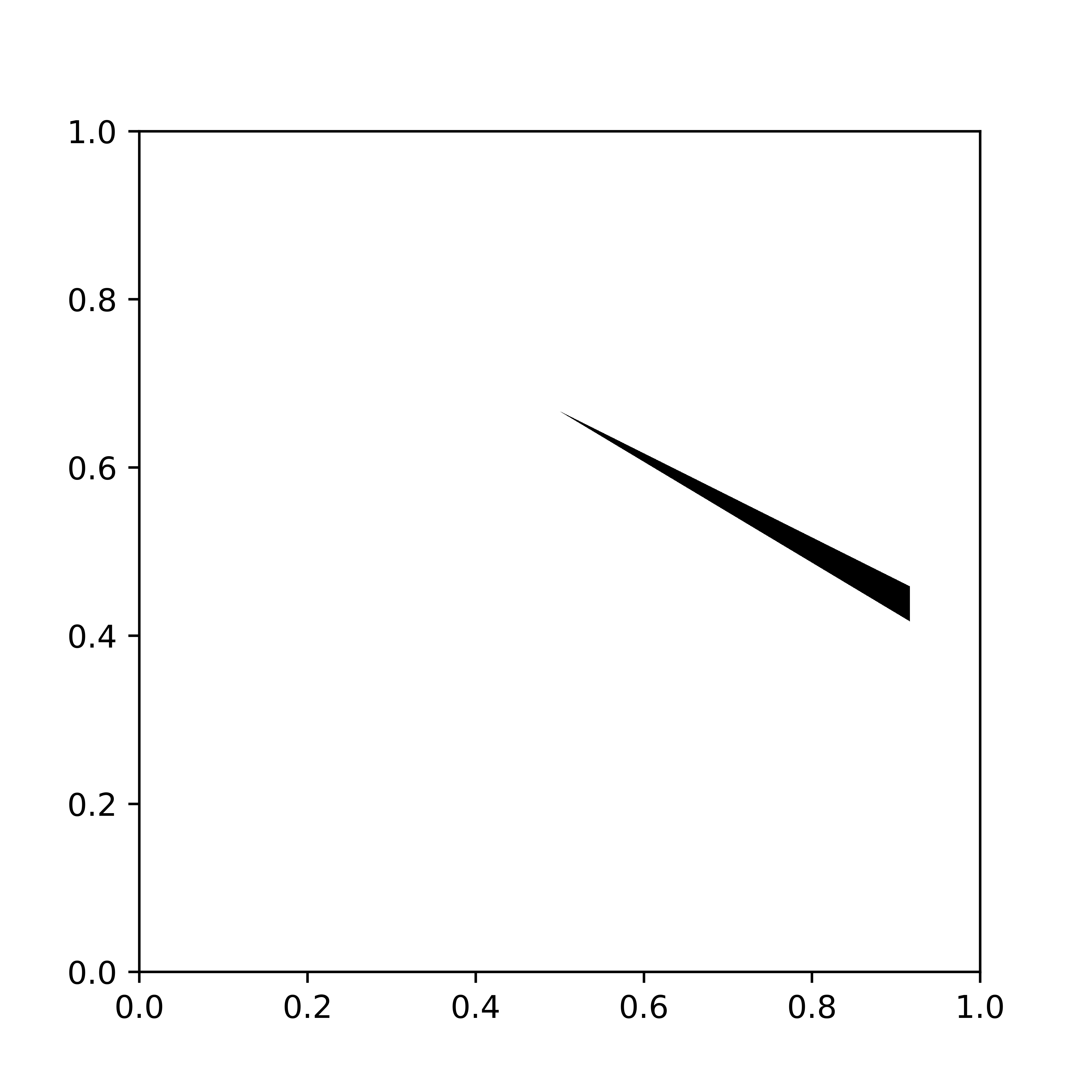
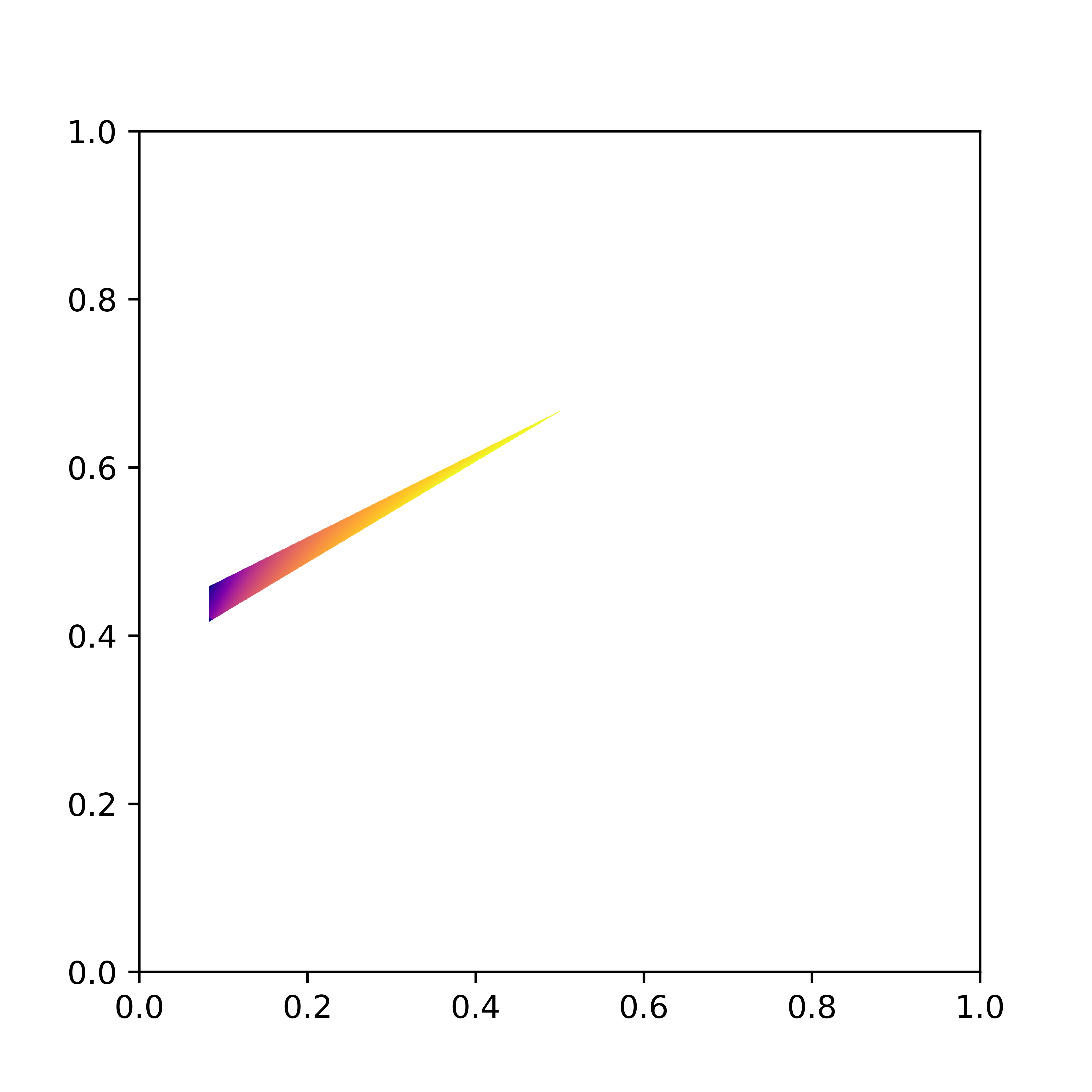
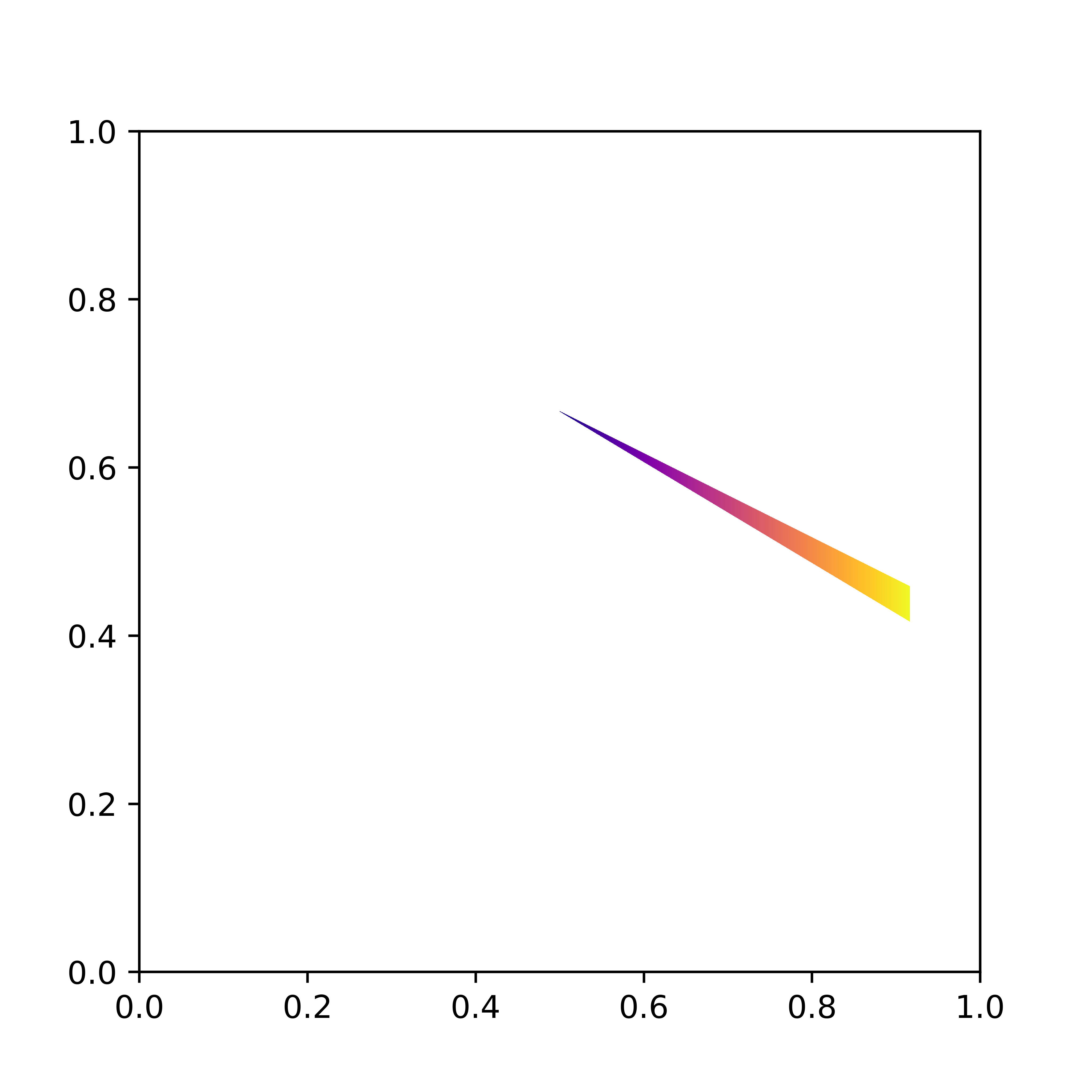
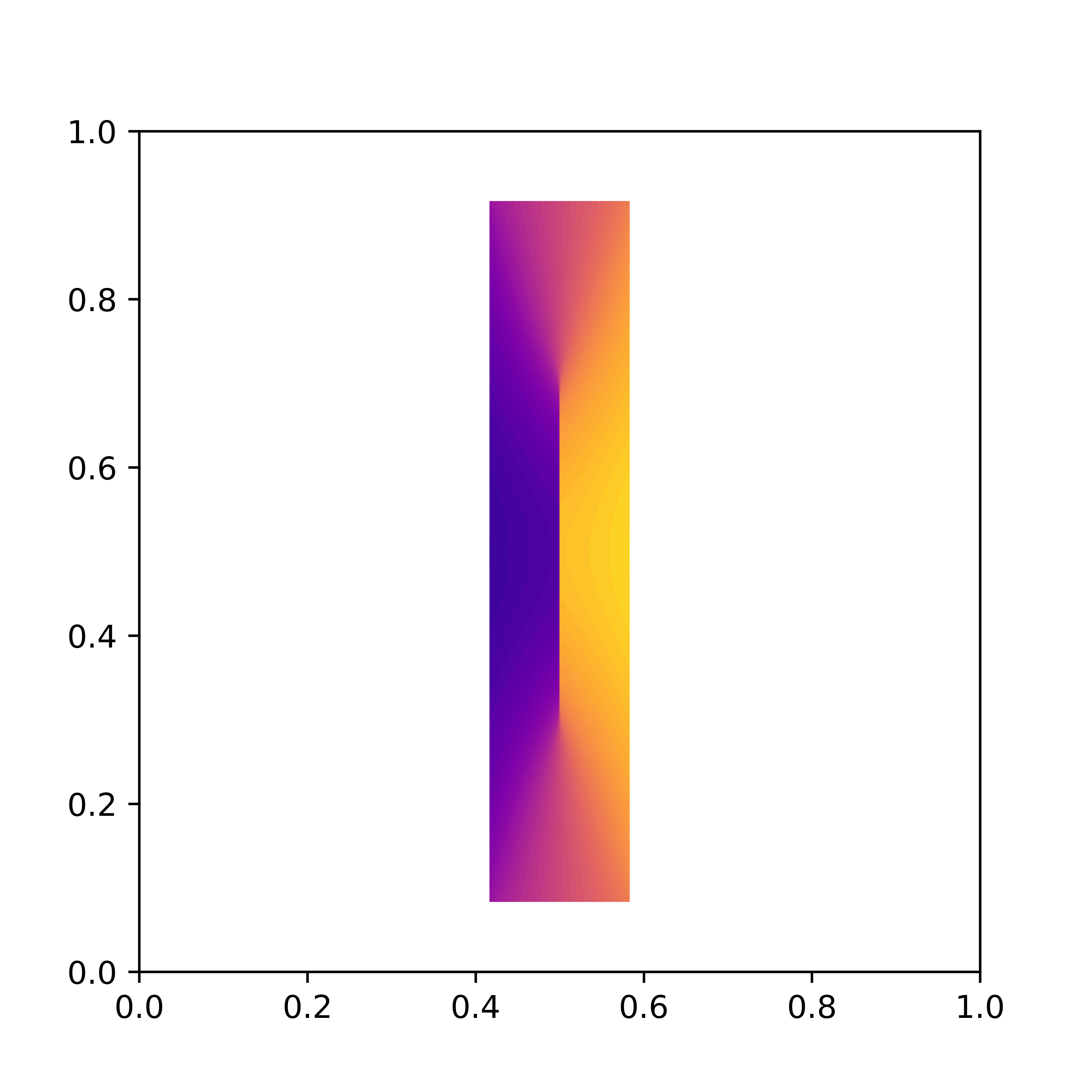
Santambrogio–Wang's counterexample

In [4] Santambrogio and Wang showed that the displacement interpolant between two uniform measures supported on convex domains needs not be supported on convex domains. The following shows snapshots at time t=0, t=1/2 and t=1 of their counterexample. Note indeed that the initial and final measures (t=0 and t=1 respectively) are supported on a convex shape (a triangle) while the displacement interpolation at t=1/2 is not.

Santambrogio-Wang's initial density
Time t=0.
Santambogio-Wang's barycenter
Time t=1/2.
Santambogio-Wang's final density
Time t=1.

Below we show how mass is transported optimally from the initial measure to the final measure.

Santambrogio-Wang's xMap
Support of the initial density. Colors represent the mapping from initial density to final density.
Santambogio-Wang's xMap
Support of the final density.

Rectangle to ring

xMap
Support of the initial density. Colors represent the mapping from initial density to final density.
xId
Support of the final density.

References

[1] Matt Jacobs and Flavien Léger. A fast approach to optimal transport: The back-and-forth method. 2019.

[2] Robert McCann. A convexity principle for interacting gasses. Advances in mathematics 128 (1997), 153-179.

[3] Luis A. Caffarelli. The regularity of mappings with a convex potential. J. Amer. Math. Soc. 5, 1 (1992), 99–104.

[4] Filippo Santambrogio and Xu-Jia Wang. Convexity of the support of the displacement interpolation: Counterexamples. Appl. Math. Letters 58 (2016), 152–158.